One philosophical reason for categorification is that it refines our concept of ‘sameness’ by allowing us to distinguish between isomorphism and equality. In a set, two elements are either the same or different. In a category, two objects can be ‘the same in a way’ while still being different. In other words, they can be isomorphic but not equal. Even more importantly, two objects can be the same in more than one way, since there can be different isomorphisms between them. This gives rise to the notion of the ‘symmetry group’ of an object: its group of automorphisms.
Consider, for example, the fundamental groupoid Π1(X) of a topological space X: the category with points of X as objects and homotopy classes of paths with fixed endpoints as morphisms. This category captures all the homotopy-theoretic information about X in dimensions ≤ 1. The group of automorphisms of an object x in this category is just the fundamental group π1(X,x). If we decategorify the fundamental groupoid of X, we forget how points in X are connected by paths, remembering only whether they are, and we obtain the set of components of X. This captures only the homotopy 0-type of X.
This example shows how decategorification eliminates ‘higher-dimensional information’ about a situation. Categorification is an attempt to recover this information. This example also suggests that we can keep track of the homotopy 2-type of X if we categorify further and distinguish between paths that are equal and paths that are merely isomorphic (i.e., homotopic). For this we should work with a ‘2-category’ having points of X as objects, paths as morphisms, and certain equivalence classes of homotopies between paths as 2-morphisms. In a marvelous self-referential twist, the definition of ‘2-category’ is simply the categorification of the definition of ‘category’. Like a category, a 2-category has a class of objects, but now for any pair x,y of objects there is no longer a set hom(x,y); instead, there is a category hom(x,y). Objects of hom(x,y) are called morphisms of C, and morphisms between them are called 2-morphisms of C. Composition is no longer a function, but rather a functor:
◦: hom(x, y) × hom(y, z) → hom(x, z)
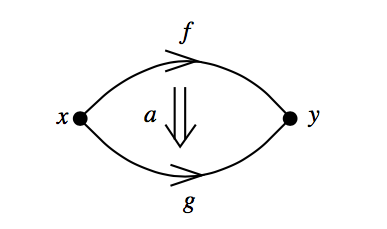
For any object x there is an identity 1x ∈ hom(x,x). And now we have a choice. On the one hand, we can impose associativity and the left and right unit laws strictly, as equational laws. If we do this, we obtain the definition of ‘strict 2-category’. On the other hand, we can impose them only up to natural isomorphism, with these natural isomorphisms satisfying the coherence. This is clearly more compatible with the spirit of categorification. If we do this, we obtain the definition of ‘weak 2-category’. (Strict 2-categories are traditionally known as ‘2-categories’, while weak 2-categories are known as ‘bicategories’.)
The classic example of a 2-category is Cat, which has categories as objects, functors as morphisms, and natural transformations as 2-morphisms. The presence of 2-morphisms gives Cat much of its distinctive flavor, which we would miss if we treated it as a mere category. Indeed, Mac Lane has said that categories were originally invented, not to study functors, but to study natural transformations! A good example of two functors that are not equal, but only naturally isomorphic, are the identity functor and the ‘double dual’ functor on the category of finite-dimensional vector spaces. Given a topological space X, we can form a 2-category Π>sub>2(X) called the ‘fundamental 2-groupoid’ of X. The objects of this 2-category are the points of X. Given x, y ∈ X, the morphisms from x to y are the paths f: [0,1] → X starting at x and ending at y. Finally, given f, g ∈ hom(x, y), the 2-morphisms from f to g are the homotopy classes of paths in hom(x, y) starting at f and ending at g. Since the associative law for composition of paths holds only up to homotopy, this 2-category is a weak 2-category. If we decategorify the fundamental 2-groupoid of X, we obtain its fundamental groupoid.
From 2-categories it is a short step to dreaming of n-categories and even ω-categories — but it is not so easy to make these dreams into smoothly functioning mathematical tools. Roughly speaking, an n-category should be some sort of algebraic structure having objects, 1-morphisms between objects, 2-morphisms between 1-morphisms, and so on up to n-morphisms. There should be various ways of composing j-morphisms for 1 ≤ j ≤ n, and these should satisfy various laws. As with 2-categories, we can try to impose these laws either strictly or weakly.
Other approaches to n-categories use j-morphisms with other shapes, such as simplices, or opetopes. We believe that there is basically a single notion of weak n-category lurking behind these different approaches. If this is true, they will eventually be shown to be equivalent, and choosing among them will be merely a matter of convenience. However, the precise meaning of ‘equivalence’ here is itself rather subtle and n-categorical in flavor.
The first challenge to any theory of n-categories is to give an adequate treatment of coherence laws. Composition in an n-category should satisfy equational laws only at the top level, between n-morphisms. Any law concerning j-morphisms for j < n should hold only ‘up to equivalence’. Here a n-morphism is defined to be an ‘equivalence’ if it is invertible, while for j < n a j-morphism is recursively defined to be an equivalence if it is invertible up to equivalence. Equivalence is generally the correct substitute for the notion of equality in n-categorical mathematics. When laws are formulated as equivalences, these equivalences should in turn satisfy coherence laws of their own, but again only up to equivalence, and so on. This becomes ever more complicated and unmanageable with increasing n unless one takes a systematic approach to coherence laws.
The second challenge to any theory of n-categories is to handle certain key examples. First, for any n, there should be an (n + 1)-category nCat, whose objects are (small) n-categories, whose morphisms are suitably weakened functors between these, whose 2-morphisms are suitably weakened natural transformations, and so on. Here by ‘suitably weakened’ we refer to the fact that all laws should hold only up to equivalence. Second, for any topological space X, there should be an n-category Πn(X) whose objects are points of X, whose morphisms are paths, whose 2-morphisms are paths of paths, and so on, where we take homotopy classes only at the top level. Πn(X) should be an ‘n-groupoid’, meaning that all its j-morphisms are equivalences for 0 ≤ j ≤ n. We call Πn(X) the ‘fundamental n-groupoid of X’. Conversely, any n-groupoid should determine a topological space, its ‘geometric realization’.
In fact, these constructions should render the study of n-groupoids equivalent to that of homotopy n-types. A bit of the richness inherent in the concept of n-category becomes apparent when we make the following observation: an (n + 1)-category with only one object can be regarded as special sort of n-category. Suppose that C is an (n+1)-category with one object x. Then we can form the n-category C ̃ by re-indexing: the objects of C ̃ are the morphisms of C, the morphisms of C ̃ are the 2-morphisms of C, and so on. The n-categories we obtain this way have extra structure. In particular, since the objects of C ̃ are really morphisms in C from x to itself, we can ‘multiply’ (that is, compose) them.
The simplest example is this: if C is a category with a single object x, C ̃ is the set of endomorphisms of x. This set is actually a monoid. Conversely, any monoid can be regarded as the monoid of endomorphisms of x for some category with one object x. We summarize this situation by saying that ‘a one-object category is a monoid’. Similarly, a one-object 2-category is a monoidal category. It is natural to expect this pattern to continue in all higher dimensions; in fact, it is probably easiest to cheat and define a monoidal n-category to be an (n + 1)-category with one object.
Things get even more interesting when we iterate this process. Given an (n + k)-category C with only one object, one morphism, and so on up to one (k − 1)-morphism, we can form an n-category whose j-morphisms are the (j + k)-morphisms of C. In doing so we obtain a particular sort of n-category with extra structure and properties, which we call a ‘k-tuply monoidal’ n-category. Table below shows what we expect these to be like for low values of n and k. For example, the Eckmann-Hilton argument shows that a 2-category with one object and one morphism is a commutative monoid. Categorifying this argument, one can show that a 3-category with one object and one morphism is a braided monoidal category. Similarly, we expect that a 4-category with one object, one morphism and one 2-morphism is a symmetric monoidal category, though this has not been worked out in full detail, because of our poor understanding of 4-categories. The fact that both braided and symmetric monoidal categories appear in this table seems to explain why both are natural concepts.

In any reasonable approach to n-categories there should be an n-category nCatk whose objects are k-tuply monoidal weak n-categories. One should also be able to treat nCatk as a full sub-(n + k)-category of (n + k)Cat, though even for low n, k this is perhaps not as well known as it should be. Consider for example n = 0, k = 1. The objects of 0Cat1 are one-object categories, or monoids. The morphisms of 0Cat1 are functors between one-object categories, or monoid homomorphisms. But 0Cat1 also has 2-morphisms corresponding to natural transformations.
• Decategorification: (n, k) → (n − 1, k). Let C be a k-tuply monoidal n-category C. Then there should be a k-tuply monoidal (n − 1)-category DecatC whose j-morphisms are the same as those of C for j < n − 1, but whose (n − 1)-morphisms are isomorphism classes of (n − 1)-morphisms of C.
• Discrete categorification: (n, k) → (n + 1, k). There should be a ‘discrete’ k-tuply monoidal (n + 1)-category DiscC having the j-morphisms of C as its j-morphisms for j ≤ n, and only identity (n + 1)-morphisms. The decategorification of DiscC should be C.
• Delooping: (n, k) → (n + 1, k − 1). There should be a (k − 1)-tuply monoidal (n + 1)-category BC with one object obtained by reindexing, the j-morphisms of BC being the (j + 1)-morphisms of C. We use the notation ‘B’ and call BC the ‘delooping’ of C because of its relation to the classifying space construction in topology.
• Looping: (n, k) → (n − 1, k + 1). Given objects x, y in an n-category, there should be an (n − 1)-category hom(x, y). If x = y this should be a monoidal (n−1)-category, and we denote it as end(x). For k > 0, if 1 denotes the unit object of the k-tuply monoidal n-category C, end(1) should be a (k + 1)-tuply monoidal (n − 1)-category. We call this process ‘looping’, and denote the result as ΩC, because of its relation to loop space construction in topology. For k > 0, looping should extend to an (n + k)-functor Ω: nCatk → (n − 1)Catk+1. The case k = 0 is a bit different: we should be able to loop a ‘pointed’ n-category, one having a distinguished object x, by letting ΩC = end(x). In either case, the j-morphisms of ΩC correspond to certain (j − 1)-morphisms of C.
• Forgetting monoidal structure: (n, k) → (n, k−1). By forgetting the kth level of monoidal structure, we should be able to think of C as a (k−1)-tuply monoidal n-category FC. This should extend to an n-functor F: nCatk → nCatk−1.
• Stabilization: (n, k) → (n, k + 1). Though adjoint n-functors are still poorly understood, there should be a left adjoint to forgetting monoidal structure, which is called ‘stabilization’ and denoted by S: nCatk → nCatk+1.
• Forming the generalized center: (n,k) → (n,k+1). Thinking of C as an object of the (n+k)-category nCatk, there should be a (k+1)-tuply monoidal n-category ZC, the ‘generalized center’ of C, given by Ωk(end(C)). In other words, ZC is the largest sub-(n + k + 1)-category of (n + k)Cat having C as its only object, 1C as its only morphism, 11C as its only 2-morphism, and so on up to dimension k. This construction gets its name from the case n = 0, k = 1, where ZC is the usual center of the monoid C. Categorifying leads to the case n = 1, k = 1, which gives a very important construction of braided monoidal categories from monoidal categories. In particular, when C is the monoidal category of representations of a Hopf algebra H, ZC is the braided monoidal category of representations of the quantum double D(H).
