Frege’s Ontological Correlates of Propositions

For Frege there were only two ontological correlates of propositions: the True and the False. All true propositions denote the True, and all false prepositions denote the False. From an ontological point of view, if all true propositions denote exactly one and the same entity, then the underlying philosophical position is the absolute monism of facts.

Lets disprove what Suszko called ‘Frege’s axiom’: namely the assumption that there exist only two referents for propositions.

Frege’s position on propositions was part of a more general view. Indeed, Frege adopted a principle of homogeneity (Perzanowski) according to which there are two fundamental categories of signs (Bedeutungen and truth-values) and two fundamental categories of senses (Sinn and Gedanken).

Both categories of signs (names and propositions) have sense and reference. The sense of a name is its Sinn, that way in which its referent is given, while the referent itself, the Bedeutung, is the object named by the name. As for propositions, their sense is the Gedanke, while their reference is their logical value.

Since the two semiotic triangles are entirely similar in structure, we need analyze only one of them: that relative to propositions.

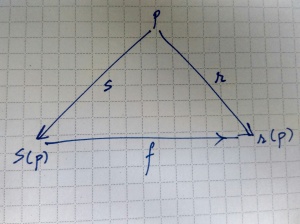
Here p is a proposition, s(p) is the sense of p, and r(p) is the referent of p. The functional composition states that s(p) is the way in which p yields r(p). The triangle has been drawn with the functions linking its vertexes explicitly shown. When the functions are composable, the triangle is said to commute, yielding

f(s(p)) = r(p), or f ° s(p) = r(p)

An interesting question now arises: is it possible to generalize the semiotic triangle? And if it is possible to do so, what is required? A first reorganization and generalization of the semiotic triangle therefore involves an explicit differentiation between the truth-value assigning function and the referent assigning function. We thus have the following double semiotic triangle:

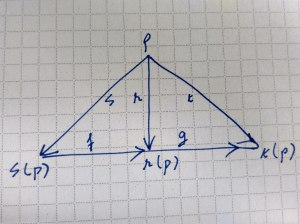
where r stands for the referent assigning function and t for the truth-value assigning function. Extending the original semiotic triangle by also considering utterances:

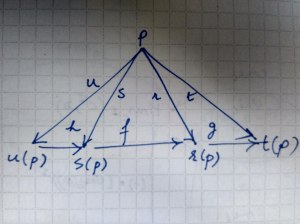
Suszko uses the terms logical valuations for the procedures that assign truth-values, and algebraic valuations for those that assign referents. By arguing for the existence of only two referents, Frege ends up by collapsing logical and algebraic valuations together, thereby rendering them indistinguishable.

Having generalized the semiotic triangle into the double semiotic triangle, we must now address the following questions:

1. when do two propositions have the same truth value?
2. when do two propositions have the same referent?
3. when do two propositions have the same sense?

Sameness of logical value will be denoted by ↔ (logical equivalence), while sameness of referent will be indicated with ≡ (not to be confused with the equiform ≡ to express indiscernibility) and sameness of sense (synonymy) by ≈. Two propositions are synonymous when they have the same sense:

(p ≈ q) = 1 iff (s(p) = s(q)) = 1

Two propositions are identical when they have the same referent:

(p ≡ q) = 1 iff (r(p) = r(q)) = 1

Two propositions are equivalent when they have the same truth value:

(p ↔ q) = 1 iff (t(p) = t(q)) = 1

These various concepts are functionally connected as follows:

s(p) = s(q) implies r(p) = r(q), r(p) = r(q) implies t(p) = t(q)

In general, the constraints that we impose on referents correspond to the ontological assumptions that characterize the theory. The most general logic of all is the one that imposes no restriction at all on r valuations. Just as Fregean logic recognizes only two referents so the most general logic recognizes more than numerable set of them. Between these two extremes, of course, there are numerous intermediate cases. Pure non-Fregean logic is extremely weak, a chaos. If it is to yield something, it has to be strengthened.

 

Mereology

Theory of parts and the whole concern both formal and material ontologies. It pertains to the former as a pure theory of independence and non-independence, and to the latter as regards the particular laws of non-independence that apply in the various ontological regions.

Mereologies are generally classified into extensional and intensional, where the former are ontologically monistic: every object that exists is an object; the parts of objects are objects; and the compositions of objects are objects as well. This is the position put forward by Stanisław Leśniewski, who starts from his definition of ontology where he gives formal definition of the concept of ‘object’ and then extends it in his concert of mereology based on the concept of being a ‘proper part of’, then developing it further in his theory of space and time. Intensional mereologies, by contrast distinguish the parts of an entity into independent and non-independent parts. The former are termed ‘pieces’, and they are those that effectively assume the denomination ‘part’, while the latter are called ‘moments’. From an ontological point of view, parts are objects in the same sense that the entities of which they are parts are objects. Moments have a different ontological valence. they are secondary objectualities and solely in the translated and subjective sense. Which, however, do not mean arbitrary. Note the formulation employed by Husserl, who speaks of the independence of parts and the non-independence of moments, not of independence and dependence. The difference is a subtle one, but it is deliberately introduced. The reason for it resides in Husserl’s mathematical training, where the use of negation is that these cases signify that equality is possible. where a is said to be not greater than b, this means that a is less than b or is equal to b. Translated into the present scenario, when one says that a is non-independent of b, the intention is to say that a is dependent on b or that a is equal to b. Moments, may therefore be equal to the whole of which they are moments, where, however, the concept of equality should be understood in the sense of indiscernibility. The possible indiscernibility of the moments from the whole should not be confused with the possible identity of the part with the whole. A part may even be the whole itself, whereas the moment can at most coincide with the whole; or it may be indiscernible from the whole, but is nonetheless distinct from it.