Conjuncted here.
The topology of the World Trade, which is encapsulated in its adjacency matrix aij defined by
aij(t) ≡ 1 if fij(t) > 0
aij(t) ≡ 0 if fij(t) = 0
, strongly depends on the GDP values wi. Indeed, the problem can be mapped onto the so-called fitness model where it is assumed that the probability pij for a link from i to j is a function p(xi, xj) of the values of a fitness variable x assigned to each vertex and drawn from a given distribution. The importance of this model relies in the possibility to write all the expected topological properties of the network (whose specification requires in principle the knowledge of the N2 entries of its adjacency matrix) in terms of only N fitness values. Several topological properties including the degree distribution, the degree correlations and the clustering hierarchy are determined by the GDP distribution. Moreover, an additional understanding of the World Trade as a directed network comes from the study of its reciprocity, which represents the strong tendency of the network to form pairs of mutual links pointing in opposite directions between two vertices. In this case too, the observed reciprocity structure can be traced back to the GDP values.
The probability that at time t a link exists from i to j (aij = 1) is empirically found to be
pt [xi(t), xj(t)] = [α(t) xi(t) xj(t)]/[1 + β(t) xi(t) xj(t)]
where xi is the rescaled GDP and the parameters α(t) and β(t) can be fixed by imposing that the expected number of links
Lexp(t) = ∑i≠j pt [xi(t), xj(t)]
equals its empirical value
L(t) = ∑i≠j aij(t)
and that the expected number of reciprocated links
L↔exp(t) = ∑i≠j pt[xi(t), xj(t)] pt[xj(t), xi(t)]
equals its observed value
L↔(t) = ∑i≠j aij(t) aji(t)
This particular structure of the World Trade topology can be tested by comparing various expected topological properties with the empirical ones. For instance, we can compare the empirical and the theoretical plots of vertex degrees (at time t) versus their rescaled GDP xi(t). Note that since pt [xi(t), xj(t)] is symmetric under the exchange of i and j, at any given time the expected in-degree and the expected out-degree of a vertex i are equal. We denote both by kexpi, which can be expressed as
kexpi(t) = ∑j≠i pt[xi(t), xj(t)]
Since the number of countries N(t) increases in time, we define the rescaled degrees
k ̃i(t) ≡ ki(t)/[N(t) − 1]
that always represent the fraction of vertices which are connected to i (the term −1 comes from the fact that there are no self-loops in the network, hence the maximum degree is always N − 1). In this way, we can easily compare the data corresponding to different years and network sizes. The results are shown in the figure below for various snapshots of the system.
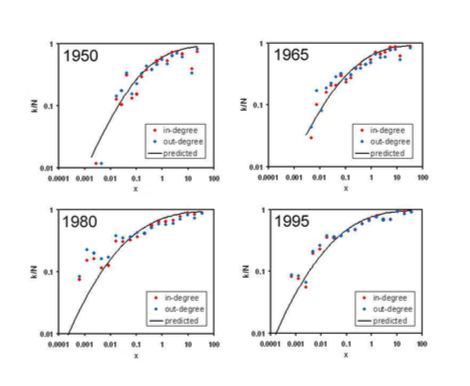
Figure: Plot of the rescaled degrees versus the rescaled GDP at four different years, and comparison with the expected trend.
The empirical trends are in accordance with the expected ones. Then we can also compare the cumulative distribution Pexp>(k ̃exp) of the expected degrees with the empirical degree distributions Pin>(k ̃in) and Pout>(k ̃out). The results are shown in the following figure and are in conformity to a good agreement between the theoretical prediction and the observed behavior.

Figure: Cumulative degree distributions of the World Trade topology for four different years and comparison with the expected trend.
Note that the accordance with the predicted behaviour is extremely important since the expected quantities are computed by using only the N GDP values of all countries, with no information regarding the N2 trade values. On the other hand, the empirical properties of the World Trade topology are extracted from trade data, with no knowledge of the GDP values. The agreement between the properties obtained by using these two independent sources of information is therefore surprising. This also shows that the World Trade topology crucially depends on the GDP distribution ρ(x).
